Triangles are the unsung heroes of geometry, lurking in every corner of our world. But when it comes to the Pythagorean theorem, many wonder if this classic formula is a one-size-fits-all solution. Picture this: you’re at a party, and someone starts talking about right triangles like they’re the life of the bash. But what about those sneaky obtuse and acute triangles? Do they get to join the fun?
Table of Contents
ToggleUnderstanding the Pythagorean Theorem
The Pythagorean theorem establishes a foundational principle in geometry. It specifically relates to right triangles, defining a relationship between their sides.
Definition and Formula
The theorem states that, in a right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. This relationship can be written as ( a^2 + b^2 = c^2 ), where ( c ) represents the hypotenuse, while ( a ) and ( b ) denote the other sides. For example, if one side measures 3 units and the other side 4 units, the hypotenuse calculates as ( sqrt{3^2 + 4^2} ), equating to 5 units.
Historical Background
The Pythagorean theorem dates back to ancient civilizations, with evidence in Babylonian tablets around 2000 BCE. Early mathematicians like Pythagoras popularized the concept in ancient Greece. Scholars adopted and documented the theorem across cultures, confirming its universal application for right triangles. Throughout history, various proofs evolved, reinforcing its significance in mathematics and architecture.
Applicability to Different Types of Triangles
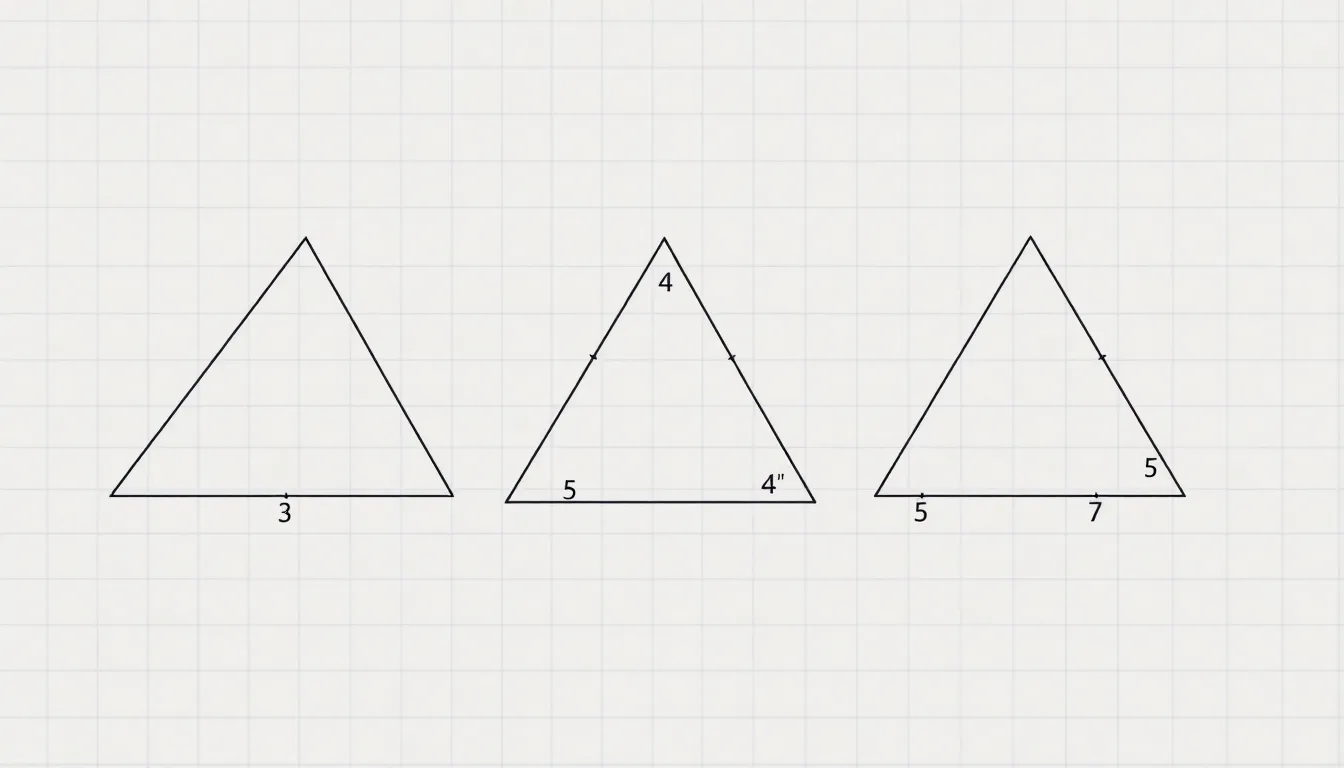
The Pythagorean theorem primarily applies to right triangles, while its applicability varies for obtuse and acute triangles.
Right Triangles
Right triangles perfectly exemplify the Pythagorean theorem. This theorem states that in these triangles, the square of the hypotenuse length equals the sum of the squares of the other two side lengths, represented as a² + b² = c². To illustrate, a triangle with side lengths of 3 and 4 units leads to a hypotenuse of 5 units. The theorem consistently provides accurate calculations for right triangles due to the inherent properties of their angles, ensuring reliability in various applications.
Obtuse Triangles
Obtuse triangles do not conform to the Pythagorean theorem. Although they contain an angle greater than 90 degrees, the sum of the squares of the shorter sides does not equal the square of the longest side. For instance, in an obtuse triangle with sides measuring 3, 4, and 6 units, the relationship a² + b² (3² + 4² = 25) fails to match c² (6² = 36). Therefore, using the Pythagorean theorem for obtuse triangles leads to inaccuracies and miscalculations.
Acute Triangles
Acute triangles also challenge the Pythagorean theorem. These triangles feature all angles less than 90 degrees, which impacts the relationship among their sides. While the theorem does not directly apply, it can still offer insights. In acute triangles, the sum of the squares of the two shorter sides remains greater than the square of the longest side. Given a triangle with side lengths of 5, 6, and 7, a² + b² (5² + 6² = 61) exceeds c² (7² = 49). This observation emphasizes that while the theorem doesn’t apply succinctly, its concepts help analyze side relationships in acute triangles.
Conditions for the Pythagorean Theorem
The Pythagorean theorem applies under specific conditions, mostly pertaining to right triangles. Understanding these criteria clarifies when the theorem is relevant.
Side Lengths and Angles
Triangles consist of three sides and three angles, which interact crucially. Right triangles showcase a unique relationship among their sides. A right triangle features one angle measuring 90 degrees, allowing the theorem to hold true where c² equals a² plus b². In contrast, obtuse triangles contain an angle greater than 90 degrees, breaking the theorem’s applicability. Acute triangles, characterized by all angles being less than 90 degrees, also present calculations that don’t align with the theorem precisely. Although direct application isn’t possible for such triangles, analyzing relationships among side lengths becomes feasible through derivative principles.
Non-Euclidean Geometries
Non-Euclidean geometries offer intriguing insights beyond traditional frameworks. Within curved spaces, like spherical or hyperbolic geometry, the Pythagorean theorem encounters limitations. In spherical geometry, for instance, the sum of angles exceeds 180 degrees, altering triangle characteristics significantly. As a result, the theorem’s fundamental relationship does not hold. In hyperbolic geometry, triangle properties vary as well, with sides diverging from Euclidean norms. Exploring these geometries expands understanding of triangular relationships beyond basic Euclidean principles, revealing broader applications and constraints of the Pythagorean theorem.
Common Misconceptions
Many people believe the Pythagorean theorem applies universally to all triangles. This misconception undermines the theorem’s specific relevance to right triangles.
Misunderstanding Triangle Types
Lumping all triangles together can lead to confusion. Right triangles are characterized by a 90-degree angle, making the theorem applicable. Obtuse triangles include an angle greater than 90 degrees, where traditional calculations do not hold true. Acute triangles, defined by all angles being less than 90 degrees, also complicate matters. While they challenge the theorem’s direct application, understanding their side relationships can still glean insights from the theorem.
Application Beyond Right Triangles
Applying the Pythagorean theorem beyond right triangles can mislead interpretations. Spherical geometry illustrates how triangle angles sum to more than 180 degrees, complicating side relationships significantly. Hyperbolic geometry introduces even more deviation from traditional Euclidean principles. In these contexts, reliance on the theorem may yield incorrect conclusions. Recognizing these limitations broadens the understanding of triangular relationships, essential for anyone studying advanced geometry.
The Pythagorean theorem serves as a crucial tool in understanding right triangles but doesn’t extend its applicability to obtuse or acute triangles. While the theorem provides a clear relationship for right triangles, its limitations become evident in other types.
In obtuse triangles the relationship among sides diverges from the theorem’s principles, and acute triangles present unique challenges that require alternative approaches.
Exploring non-Euclidean geometries further emphasizes these constraints and highlights the need for a broader understanding of triangular relationships. Recognizing these nuances is essential for anyone venturing into the complexities of geometry.






